Instance Normalization
实例归一化最初用于图像风格迁移的生成任务,按照每个图像的每一个通道维度进行归一化操作
Batch Normalization(每个通道维度,计算batch内所有样本的统计结果):
ytijk=σi2+ϵxtijk−μi
μi=HWT1∑t=1T∑l=1W∑m=1Hxtilm
σi2=HWT1∑t=1T∑l=1W∑m=1H(xtilm−μi)2
Instance Normalization(每个样本,每个通道,计算统计结果):
ytijk=σti2+ϵxtijk−μti
μti=HW1∑l=1W∑m=1Hxtilm
σti2=HW1∑l=1W∑m=1H(xtilm−μti)2
DAIN是时序预测领域的自适应归一化方法。
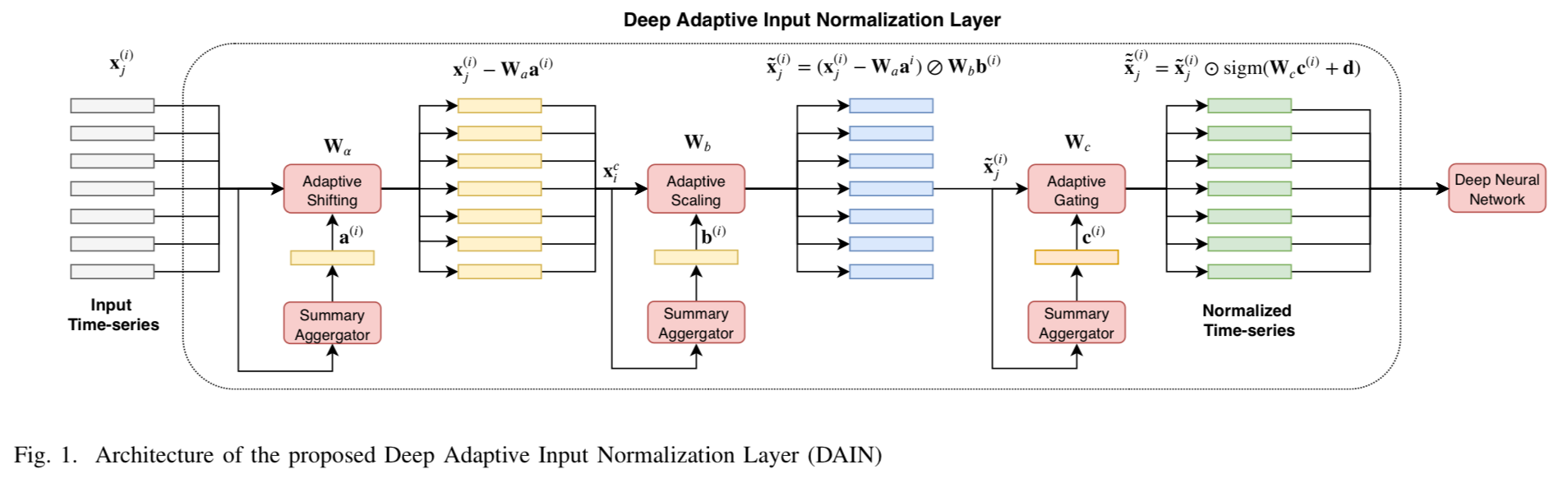
对于时间序列数据集{Xi∈Rd×L;i=1,…,N},将归一化过程拆分成三个步骤:
- 对原始数据进行平移(shifting)
αi=Waai∈Rd
ai=L1∑j=1Lxji∈Rd
- 对平移结果进行缩放(scaling)
βi=Wbbi∈Rd
bki=L1∑j=1L(xjki−αki)2,k=1,…,d
- 额外的(非线形)门控过程,抑制无关特征的影响
x~~ji=x~ji⊙γi
γi=sigmoid(Wcci+b)∈Rd
ci=L1∑j=1Lx~ji∈Rd
x~ji=(xji−αi)⊘βi
第一步、第三步仍然需要统计完整序列的均值信息
